Understanding distributed time using Vector Clocks
To build a strong foundation in distributed systems, it’s essential to first understand the concept of distributed time. Friedemann Mattern’s 1988 paper “Virtual Time and Global States of Distributed Systems” is one of the foundational works in distributed computing, introducing key concepts that help us reason about the ordering of events and capture consistent global states in distributed systems.
Prerequisite
This blog is more useful to you if you have some understanding of time in distributed system. You can read my prev blog to understand more on it - time-clocks-and-ordering-of-events-in-distributed-systems
The core problem: No Global Now
The main problem Mattern was solving is how to take a snapshot in a distributed system. Taking a snapshot in distributed systems is analogous to 1000 ants trying to take picture of moving elephant.
Imagine three processes running independently. They send messages to each other and update their internal state. If you take a snapshot of each process at a random moment, the chances that your snapshot is in consistent state is low. Since each process is mutating, by the time you ask for snapshot reaches every process the system is already moved ahead.
Limitations of logical clock
Lamport clocks introduced the idea that you can tag events with timestamps and maintain the rule:
If event A causally precedes event B, then timestamp(A) < timestamp(B)
But the reverse doesn’t hold. If timestamp(A) < timestamp(B), we can’t be sure that A happened before B. Maybe they were concurrent.
We cannot tell the order of events by just looking at the timestamp
Vector clocks
While Leslie Lamport had previously introduced logical clocks, Mattern’s paper expanded on this by presenting vector clocks - a mechanism for tracking causality between events in distributed systems. Unlike Lamport clocks, vector clocks capture the complete causal relationship between events.
A vector clock maintains a vector of counters, one for each process in the system. When an event occurs:
- The process increments its own counter
- When sending a message, the current vector is attached
- When receiving a message, the vector is updated by taking the component-wise maximum
This mechanism allows the system to capture the partial ordering of events more precisely, enabling the detection of concurrent events and providing a more accurate representation of causality in the system.
Vector clocks algorithm
Initialization:
- Each process maintains a vector of integers
- Vector size equals number of processes in system
- All values initially set to 0
Local Event:
- Process increments its own position in vector
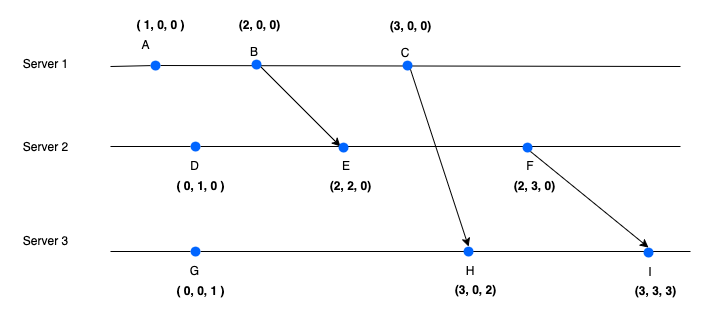
- Example: Server 1’s clock [1,0,0] → [2,0,0]
Sending Message:
- Process increments its own position
- Attaches current vector clock to message
Receiving Message:
- Takes component-wise maximum of local and received vectors
- Increments own position in resulting vector
# Vector Clock Algorithm
class Process:
def __init__(self, id, num_processes):
self.id = id
# Initialize vector clock with zeros for all processes
self.vector_clock = [0] * num_processes
def local_event(self):
# Increment own position in vector clock
self.vector_clock[self.id] += 1
def send_message(self, message):
# Increment own position before sending
self.vector_clock[self.id] += 1
# Attach current vector clock to message
return (message, self.vector_clock.copy())
def receive_message(self, message, sender_vector):
# Update vector clock:
# 1. Take component-wise maximum
# 2. Increment own position
for i in range(len(self.vector_clock)):
self.vector_clock[i] = max(self.vector_clock[i], sender_vector[i])
self.vector_clock[self.id] += 1
Comparing vector clocks
Vector clocks can be compared in three ways:
- Equal (V1 = V2):
- Two vector clocks are equal if all their components are equal
- V1[j] = V2[j] for all j
- Less than or equal (V1 ≤ V2):
- One vector clock is less than or equal to another if all components in the first are less than or equal to the corresponding components in the second
- V1[j] ≤ V2[j] for all j
- Concurrent (V1 || V2):
- Two vector clocks are concurrent if they are neither equal nor one is less than the other
- This happens when neither V1 ≤ V2 nor V2 ≤ V1 is true
def happens_before(V1, V2):
# Returns True if V1 happens before V2
less_than_exists = False
for i in range(len(V1)):
if V1[i] > V2[i]:
return False
if V1[i] < V2[i]:
less_than_exists = True
return less_than_exists
def concurrent(V1, V2):
# Returns True if V1 and V2 are concurrent
return not happens_before(V1, V2) and not happens_before(V2, V1)
Why do we care about comparing vector clocks
These comparisons are essential for:
- Determining the causal relationships between events
- Detecting concurrent operations
- Maintaining consistency in distributed systems
Optimizations in comparing vector clocks
The key optimization in vector clock comparison is that you don’t need to compare entire vectors to determine if one event happened before another. Instead, you can focus on comparing just a single component of the vector clock.
Assume we are comparing Aj, Bk. When checking if an event from process j happened before another
event, you only need to look at the j-component of both vector clocks.
This works because the j-component of a vector clock can only increase either when process j executes an event or when
there’s a chain of messages propagating from process j.
Therefore, if a later event has a larger j-component in its vector clock, it means there must be a causal relationship
(a chain of messages) connecting it to the earlier event from process j.
This significantly reduces the computational overhead since you avoid comparing entire vectors.
Vector Clock causality effect
Vector clock causality effect describes how events in a distributed system are causally related through their vector timestamps. When one event influences another through message passing or direct execution, this causal relationship is captured in their vector clocks.
Here’s how it works:
- Each event in the system gets a vector timestamp that tracks logical time across all processes
- When messages are sent between processes, the vector clock values are updated to reflect this communication
- If event A causally affects event B (meaning A happened before B and could influence it), this will be reflected in their vector clock values
- The causality is preserved because vector clock values can only increase when there’s either:
- A direct event in a process
- Message passing between processes
This mechanism ensures that if there’s any causal chain between two events (through direct execution or message passing), their vector clocks will capture this relationship. This makes vector clocks a powerful tool for tracking causality and determining the happens-before relationships between events in distributed systems.
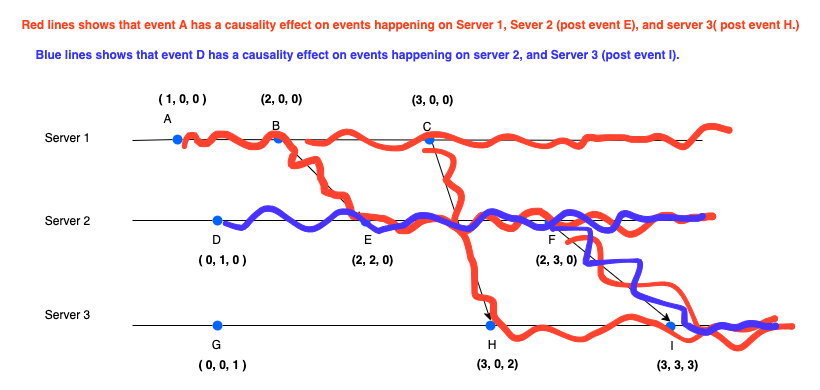
Inspiration from Minkowski relativistic space time
The vector clock model in distributed systems draws inspiration from Minkowski spacetime in Einstein’s theory of relativity. Just as Minkowski showed that simultaneity is relative—events that appear simultaneous to one observer may not be to another — vector clocks reflect that in distributed systems, there’s no absolute “now.” Instead, causality defines the structure of time. Events are ordered based on influence (cause-effect), not timestamps, just as light cones in spacetime separate causally connected events from concurrent ones.
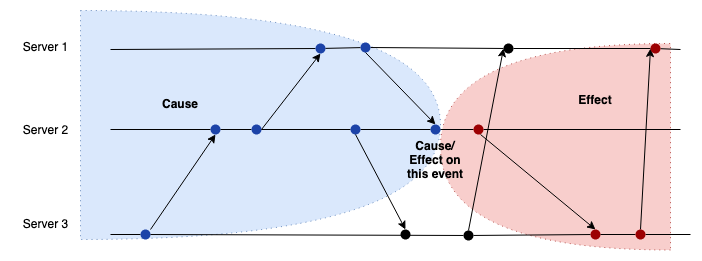
Consistent cut
Now with the basics of vector clock we can define consistent cut that can be used to get a consistent snapshot.
A consistent cut is a snapshot of a distributed computation that represents a possible global state of the system. It divides the computation into a “past” and a “future” such that if an event e is in the cut (i.e., in the past), then all events that causally precede e must also be in the cut. In other words, if the cut includes a message receipt event, it must also include the corresponding message send event. This ensures that the global state captured by the cut is meaningful and could have actually occurred during the execution of the distributed system.
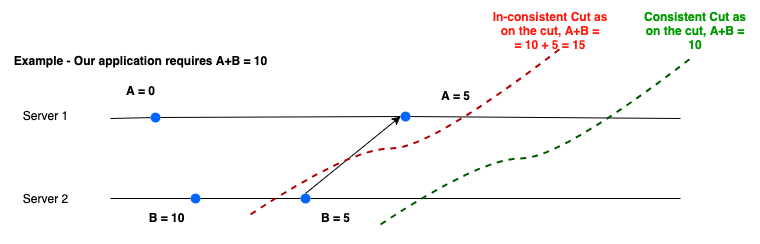
A consistent cut is a line through the distributed computation that satisfies the causality requirement:
if an event 'e' is in the cut and event 'f' happens before 'e', then 'f' must also be in the cut.
# Cut Consistency Check
def is_consistent_cut(cut_vector):
for i in range(len(processes)):
for j in range(len(processes)):
if message_sent[i][j] > cut_vector[i] and
message_received[i][j] <= cut_vector[j]:
return False
return True
Learning to take away?
The main idea that stood out to me is that in real world getting a consistent snapshot can be really powerful way to
rollback to past consistent state.
In real world when we think of simple CRUD API that has process that writes to a database and the return a message.
The process writing to database by single API call creates an illusion of things happening linearly. Its not, database is
a fully independent distributed system with its own leader and workers persisting the value in disk, replication etc.
Sending a message back to client can impact other processes. Message will have effect upon the behavior of the client.
For example - failure to send message will cause the client to retry the process. This is real world example of causality nature of distributed system.
Other key learnings to take away:
- Consistent State Capture: Learning how to capture meaningful global states in distributed systems through consistent cuts, ensuring that causality is preserved.
- Vector Clocks Importance: Recognizing that vector clocks provide a more complete solution than simple logical clocks for tracking causality relationships between events in distributed systems.
- Practical Implications: The concepts have real-world applications in taking consistent snapshots in databases.