We are on a path to build a strong foundation in distributed systems. We have already gone over distributed time; the next topic we will cover is Distributed Consensus. To build the foundation on distributed consensus, we will start with the paper ‘The Byzantine Generals Problem’ published in 1982 by Leslie Lamport, Robert Shostak, and Marshall Pease. This paper introduces the concept of Byzantine faults and formally proves the conditions under which consensus is impossible in the presence of arbitrary (malicious or faulty) behavior.

Models in Distributed system

A system model in distributed systems is a conceptual framework that defines the key characteristics, assumptions, and properties of the distributed system. It helps in understanding, designing, and reasoning about distributed systems.
Here’s a comprehensive breakdown:

  1. Node (Process) Model: Describes the behavior of computing nodes, defining how processes operate and fail. The different types of failure in nodes can be:
    • Crash failures (fail-stop)
    • Byzantine failures (arbitrary/malicious behavior)
    • Omission failures (dropped messages)
  2. Communication Model: Focuses on how messages are exchanged between nodes. It is concerned with delivery mechanism and reliability. Key characteristics:
    • Message passing vs Shared memory
    • Reliable vs Unreliable channels
    • Point-to-point vs Broadcast
    • Network partitioning possibilities
    • FIFO vs non-FIFO channels
  3. Timing Model: Focuses on time related aspects such as process execution speed, and acceptable delays, clock sync, execution rates. Key characteristics:
    • Synchronous: Fixed bounds on timing
    • Asynchronous: No timing guarantees
    • Partially synchronous: Some timing bounds

To understand system model we can use two classic thought experiments in distributed systems are: the two generals problem and the Byzantine generals problem.

The Two Generals Problem

Situation

In this thought experiment, there are two armies trying to capture a city. In order to capture the city, both the armies need to attack simultaneously. If only one army attacks, the city defeats the army.

Participants:

  1. Two armies (nodes/processes)
  2. Each general commands one army
  3. Both generals need to agree on attack time
  4. Each node can:
    • Send messages
    • Receive messages
    • Make local decisions

Node (Process) Model

In this thought experiment, our assumption is: A1: None of the generals are traitor.
A2: Our generals will not die.

Communication Model

The generals of two armies can communicate using messages. Assumptions are:
A3. message will not be tempered on the way.

Acceptable failure scenarios are:
A4. Any message can be lost on the way. Since city has strong defences, they can capture any messenger resulting in lost message.

Timing Model

A5. Messages are send asynchronously, and there is no bound on message delivery time. A6: No clocks are sync between the generals.

Bellow is the image sourced from sketch planations showcasing the thought experiment -

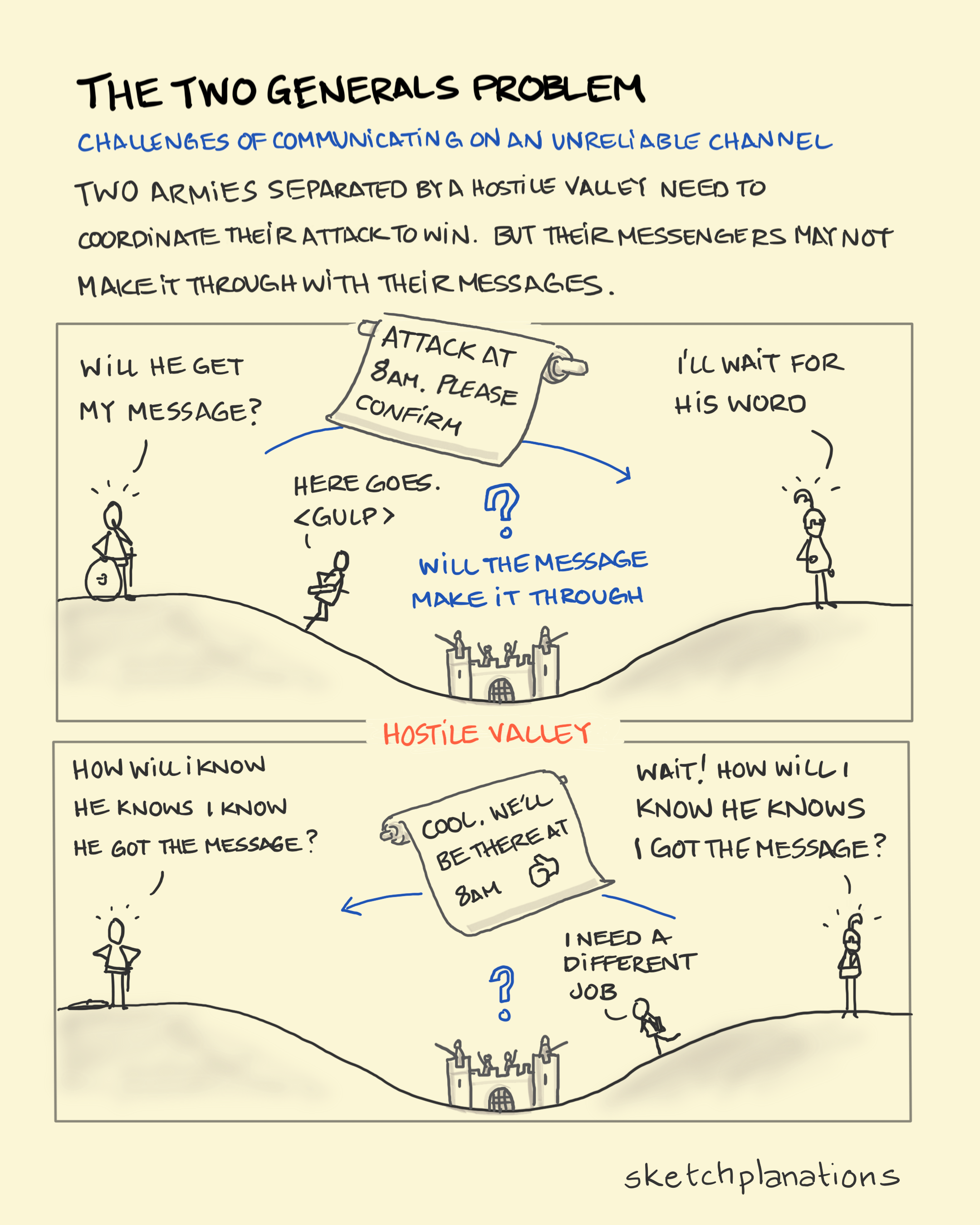
The two generals problem

“The Two Generals Problem”, highlights the core issue: reliable agreement is impossible over an unreliable channel — even if both generals want to coordinate an attack. The problem is deceptively hard.

This table shows the possible outcomes based on whether General A’s message and the acknowledgment from General B are successfully delivered:

The Two Generals Problem – Truth Table
Message from A to B Delivered? Acknowledgment from B to A Delivered? General A Attacks General B Attacks Coordinated Attack? Result
Yes Yes Yes Yes Yes ✅ City Captured
Yes No No Yes No ❌ General B Army defeated
No Yes Yes No No ❌ General A Army defeated
No N/A No No No ❌ Nothing Happens

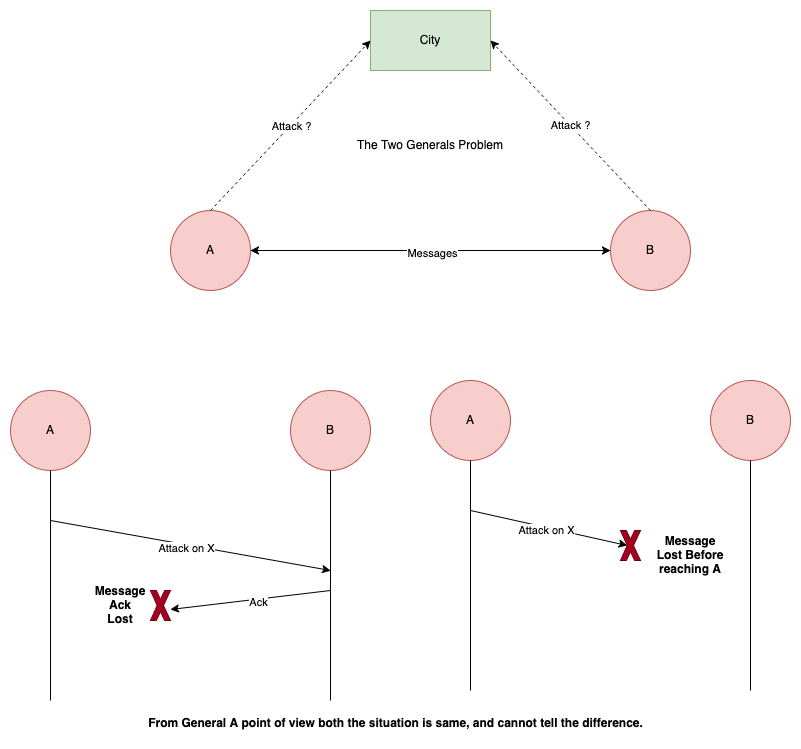
Since the network is unreliable it is impossible for General A to tell if the message is delivery and then lost, or message was not delivered. The two generals problem

Brainstorm on possible options

What protocol should the two generals use to agree on a plan ?

  1. If general A attack irrespective of acknowledgement received.
    General A can try to send lots of messages to increase the probability that one will reach the other general.
    If all messages are lost, the general A’s army will go on attack alone.

  2. General A only attacks if positive response from general B is received.
    Now General A is saved, but General B does not know if the ack is received by general A. The situation is reversed and the same problem is shifted to general B.

Learnings from this thought experiment

The core problem is no matter how many messages are exchanged, generals cannot be certain of co-ordination.

This thought experiment demonstrates that in a distributed system, there is no way for one node to have certainty about the state of another node. The only way how a node can know something is by having that knowledge communicated in a message.

The Real World Example of two generals problem

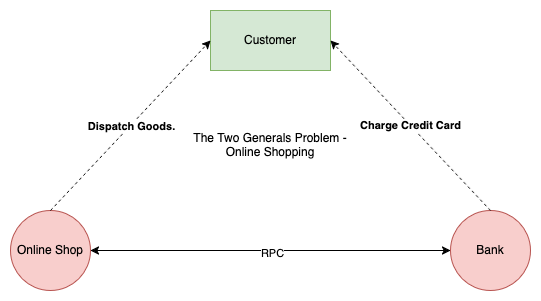
The two generals problem - practical example

The online shop has to dispatch the goods, if and only if payment goes through. To solve the problem in this scenario where customer gets charged but order did not go through. The bank will refund the customer i.e. rollback to previous state.

The fact that a payment is something that can be rolled back (unlike an army being defeated) makes the problem solvable.

The Byzantine Generals Problem

Situation

The Byzantine generals problem is similar to two generals problem. In this case, there are three or more armies trying to capture the city, messages are always delivered but there can be a traitor sending wrong messages.

Participants:

  1. n generals (nodes/processes)
  2. One commander (source node)
  3. n-1 lieutenant generals (receiving nodes)

Node (Process) Model

In this thought experiment, Nodes can be either: A1. Loyal (follows protocol) A2. Traitors (Byzantine faulty)

Communication Model

The generals of two armies can communicate using messages. Assumptions are:
A3. Message can be oral (forgeable) or signed (unforgeable signatures). A4. Messages cannot be lost/delayed.

Timing Model

A5. Messages are synchronous with fixed bound on message delivery time.

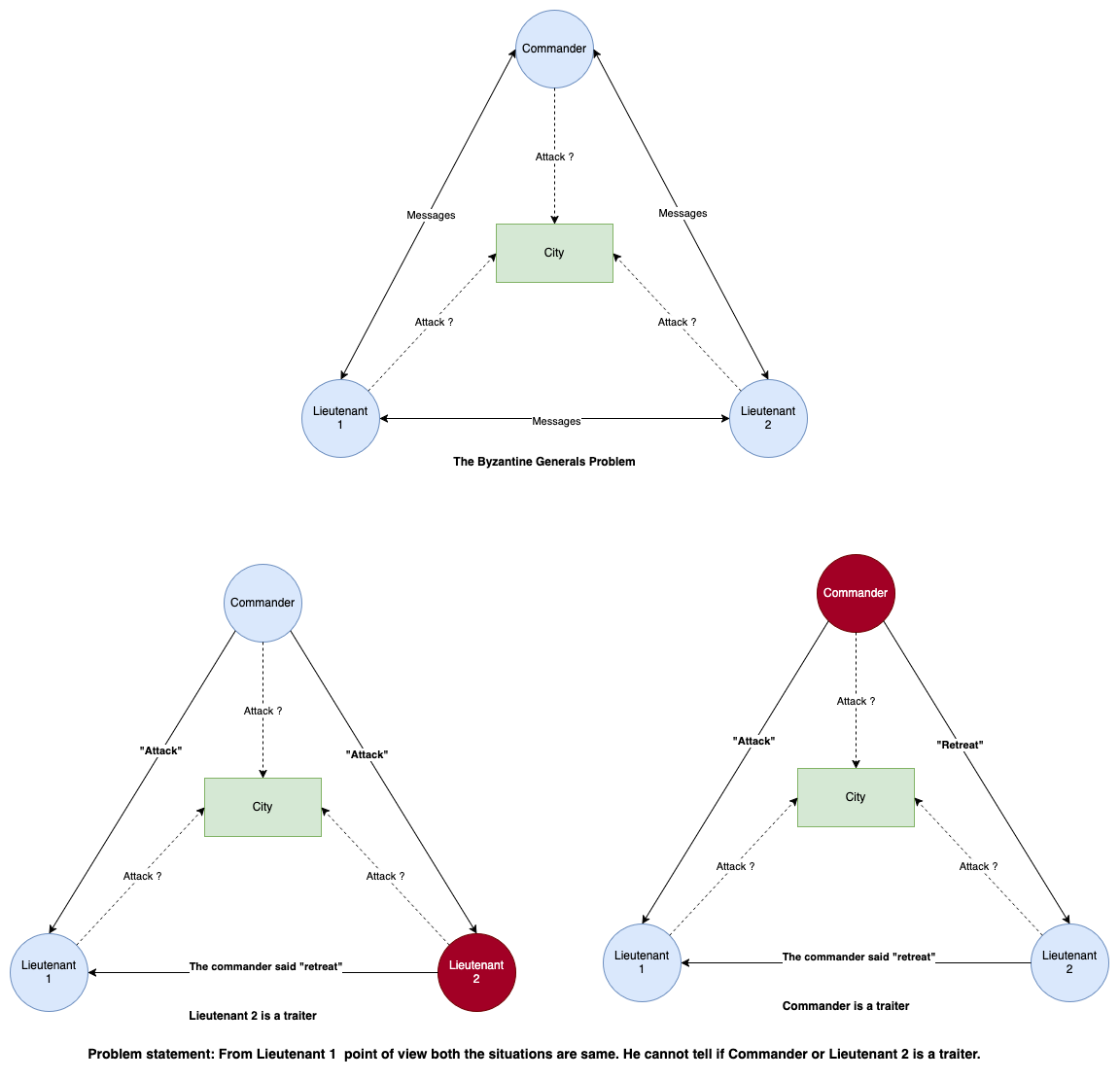
The Byzantine generals problem

Thought Experiment

We need to find an algorithm for the generals to guarantee that : A. All loyal generals decide upon the same plan of action.
B. A small number of traitors cannot cause the loyal generals to adopt a bad plan.

and more formally defining Byzantine Generals Problem. A commanding general must send an order to his n - 1 lieutenant generals such that - IC1. All loyal lieutenants obey the same order. IC2. If the commanding general is loyal, then every loyal lieutenant obeys the order he sends.

Impossibility Results
Lamport showed that if we use oral messages (can be forged), no solution will work unless more than two-thirds of the generals are loyal. For a viable solution we will need 3m + 1 generals where m is the number of traitors.

A Solution With Oral Messages

Each general is supposed to execute some algorithm that involves sending messages to the other generals, and we assume that a loyal general correctly executes his algorithm. The definition of an oral message is embodied in the following assumptions which we make for the generals’ message system:

  1. Every message that is sent is delivered correctly.
  2. The receiver of a message knows who sent it.
  3. The absence of a message can be detected.

Algorithm
To address the Byzantine Generals Problem, Lamport et al. proposed a recursive algorithm called OM(m), which stands for Oral Messages with up to m traitors. It is designed to help loyal generals reach agreement even when some of the generals may be lying, silent, or sending inconsistent messages.

Recap of the setup

  1. There is one commander and n - 1 lieutenants.
  2. The total number of generals n must be at least 3m + 1 to tolerate m traitors.
  3. Communication is synchronous and point-to-point; messages can be delayed or corrupted by traitors.

The goal is for all loyal lieutenants to agree on the same order, and if the commander is loyal, then all loyal lieutenants must follow the commander’s order.

The Byzantine generals problem algorithm

The algorithm is recursive with depth m, which is the number of traitors the system wants to tolerate.
Base Condition
If m = 0:

  1. Commander sends value to all lieutenants
  2. Lieutenants use the value received
  3. If no value received, use DEFAULT value (e.g., “Retreat”).

If m > 0 and you are the Commander:

  1. Send value to each lieutenant
  2. Wait for recursive process to complete

If m > 0 and you are a Lieutenant:

  1. Collect values from recursive process
  2. Use majority function on collected values

Recursive Process OM(m)

  1. Commander sends value v to all n lieutenants
  2. For each i (1 to n):
    • Lieutenant i acts as commander for OM(m-1)
    • Sends the value received to all other lieutenants
  3. Each lieutenant collects all n-1 values from other lieutenants
  4. Decision made using majority function on collected values

Example: OM(1)

Suppose n = 4 generals (commander + 3 lieutenants), tolerating m = 1 traitor.

  1. Round 1:
    • Commander → All Lieutenants: sends value v
  2. Round 2:
    • Each Lieutenant → All other Lieutenants: forwards received value
    • Each Lieutenant: makes decision based on majority of received values
                   Round 1: Commander sends value
                            Commander (C)
                               [v=1]
                                 │
                 ┌───────────────┼───────────────┐
                 ▼               ▼               ▼
            Lieutenant 1     Lieutenant 2     Lieutenant 3 ☠
               (L1)            (L2)            (L3)
               [v=1]           [v=1]           [v=1]
                                          (Receives but malicious)

                   Round 2: Lieutenants exchange values
            Lieutenant 1     Lieutenant 2     Lieutenant 3 ☠
               (L1)            (L2)            (L3)
                │               │                │
         ┌──────┴──────┐  ┌─────┴─────┐   ┌──────┴──────┐
         ▼             ▼  ▼           ▼   ▼             ▼
        L2            L3  L1          L3  L1           L2
      [v=1]         [v=1] [v=1]    [v=1] [v=0]     [v=0]
                                         LIES!    LIES!

                   Final Decision Making
        Lieutenant 1         Lieutenant 2         Lieutenant 3 ☠
     Values: [1,1,0]      Values: [1,1,0]      Values: [1,1,0]
     Majority(1,1,0)      Majority(1,1,0)      (Traitor/Ignored)
           ↓                    ↓                    ↓
         [v=1]                [v=1]             [Whatever]

Why does the Algorithm works ?

The recursive spreading and majority-voting help isolate lies. Even if up to m traitors are present, the loyal generals will eventually converge on the same result because:

  • The number of loyal messages outweighs the malicious ones due to the 3m + 1 requirement.
  • Traitors cannot forge messages from loyal nodes.
  • Recursive reporting allows loyal generals to compare what others received and identify inconsistencies.

This technique ensures consistency (agreement) and integrity (obey the loyal commander’s order) — the two key properties for consensus.

A Solution With Signed Messages

The traitors’ ability to lie makes the Byzantine Generals Problem so difficult. The problem becomes easier to solve if we can restrict that ability. One way to do this is to allow the generals to send unforgeable signed messages.

The algorithm for signed messages relies on the assumption that messages:

  • Cannot be forged (e.g., digital signatures),
  • Cannot be altered without detection, and
  • Can be verified by anyone (public-key cryptography model).

This means that Traitors can only choose not to send messages, but cannot alter signed messages

Algorithm Overview

  1. Round 0: Commander Stage
    • Commander signs and sends value (v) to all lieutenants
    • Format: C (where C is commander's signature)
  2. Round 1: Lieutenant Stage
    • Each lieutenant i receives message from commander
    • Lieutenant i adds signature and forwards to all other lieutenants
    • Format: C,i
  3. Round 2: Final Choice
    • Each lieutenant collects all messages
    • Makes decision based on rules below

Decision Rules

  1. If commander’s order received:
    • Use commander’s value
  2. If no order received from commander:
    • Use default value “RETREAT”
  3. If conflicting orders detected:
    • Commander proven traitor
    • Use default value “RETREAT”

Learnings

The Byzantine Generals Problem taught us that agreement under faulty or adversarial conditions requires redundancy, careful protocol design, and sometimes cryptography. These lessons underpin the design of modern consensus algorithms and fault-tolerant systems.

  1. Byzantine fault tolerant systems needs atleast 3f+1 hosts.
  2. Authentication (Signatures) changes everything and fairly reduces the complexity of problem.

References

  1. The Byzantine Generals Problem by Lamport, others in 1982
  2. Notes on Data Base Operating Systems by Jim Gray in 1977