We are on a path to build a strong foundation in distributed systems. We have already gone over distributed time; the next topic we will cover is Distributed Consensus. To build the foundation on distributed consensus, we will go over Paxos. Paxos revolutionized distributed computing by providing the first provably correct solution for achieving consensus among unreliable processors, forming the theoretical foundation for modern distributed systems and databases. Paxos is one of the most important and most difficult to understand algorithm. In this blog I will simplify and explain paxos in a very intuitive way.

Context

We have already two consensus algorithms by now - 2PC from Jim Gray, et al. in 1978 and 3PC from Dale Skeen, et al. in 1982. 2PC had a problem with getting blocked on single node failure. 3PC solved the handling of fail-stop fault model, but it does not handle cases where network is partitioned, and then re-merged with each partition leading to different conclusions.

To solve the problems in 3PC, Leslie Lamport came in with new consensus algorithm called Paxos Protocol in 1998. Paxos was the first correct protocol which was provably resilient to asynchronous networks. As we learned in FLP paper, we can tweak impossibility by changing the system model. Paxos sacrificed liveliness (guaranteed termination) over correctness.

Problem Paxos was solving

A consensus algorithm that ensures all nodes agree to one value among the proposed values. If no value is proposed, then no value should be chosen. If a value has been chosen, then processes should be able to learn the chosen value.

The safety requirements for consensus are:

  • Only a value that has been proposed may be chosen,
  • Only a single value is chosen, and
  • A process never learns that a value has been chosen unless it actually has been.

From the starting Lamport chose to solve correctness over liveliness requirement.

Agents in Paxos

There are three roles defined in paxos algorithm:

  • proposers - initiates the algorithm and proposes values,
  • acceptors - contributes to choosing from among the proposed values, and
  • learners - learns the agreed upon value.

(One process can play more than one role.)

Its better to understand the role by looking at the state diagram.

Note: Bellow is simplified version to build intuition and understand paxos the easy way. For practitioners please read the paper and implement it.

Phase 1 (milestone 1)

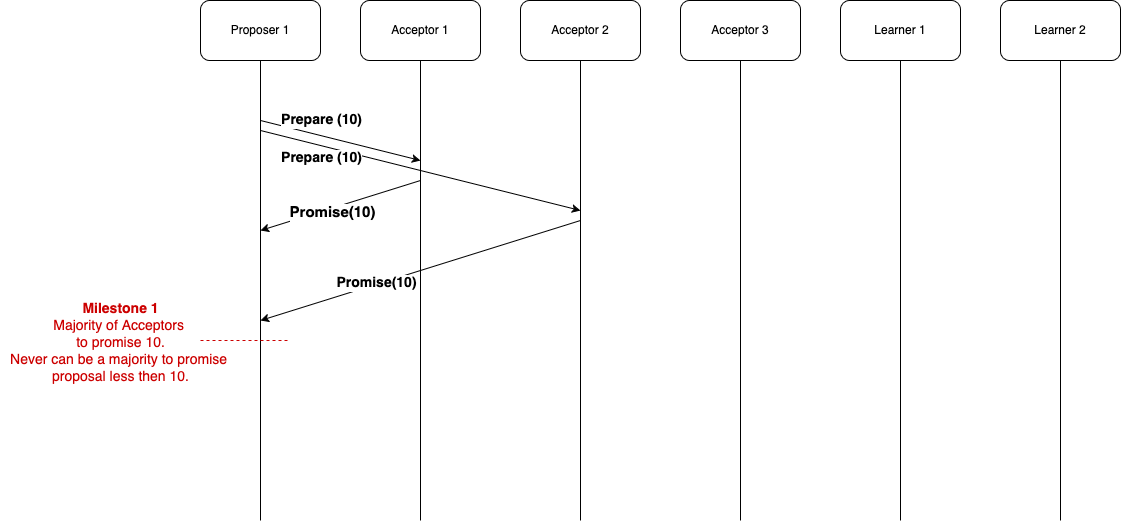
Proposer Sends prepare(n = proposal number) message to at least a majority of acceptors. Proposal number “n” must be globally unique, and higher then any proposal number that this proposer has used before.

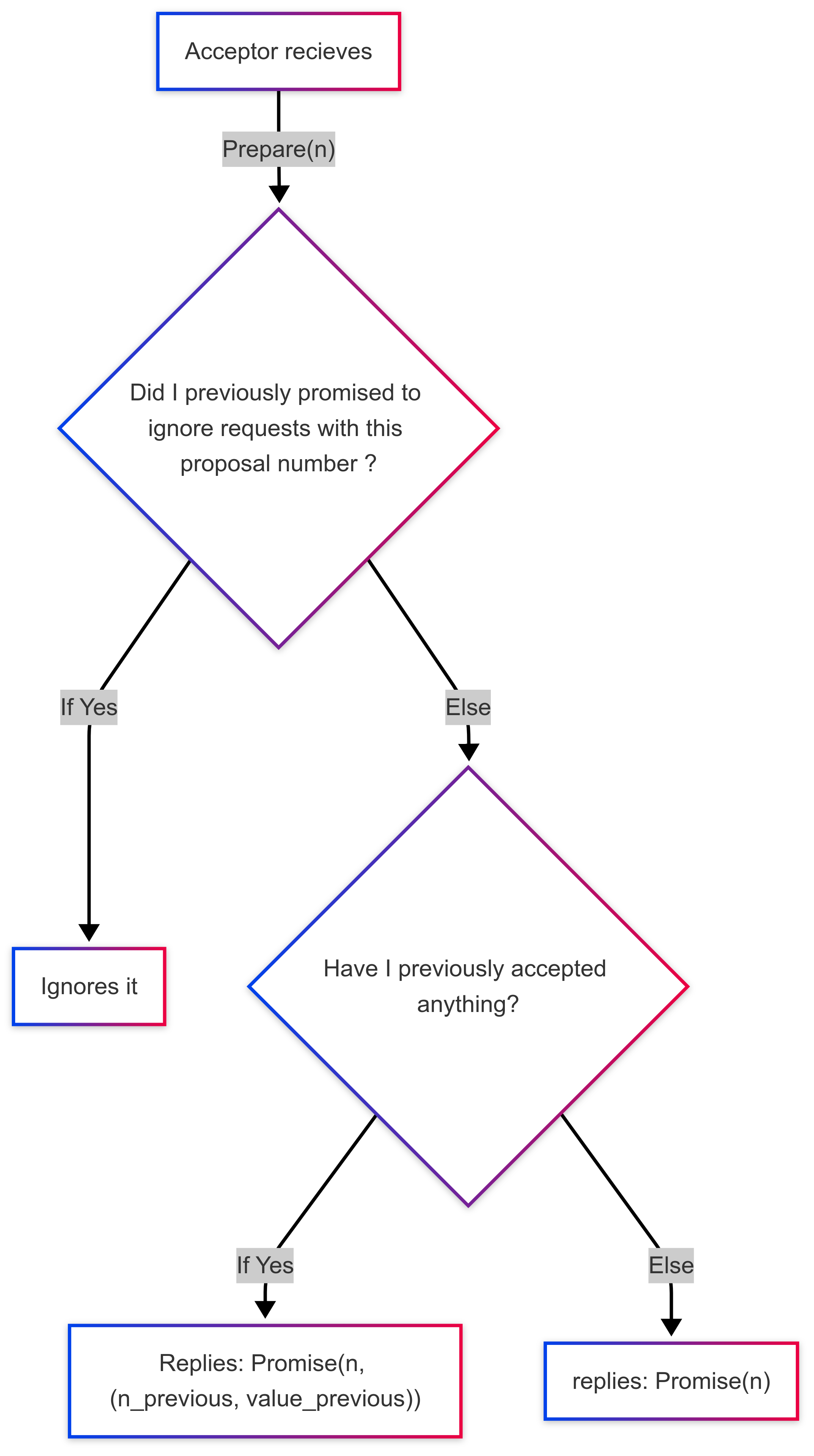
Acceptor On receiving a Prepare(n) message; It will decide if it has previously promised to ignore requests with this proposal number.

  • If so, it will ignore the message.
  • Else, it now promises to ignore any request with a proposal number lower than n and replies with Promise(n, (nprev, valueprev)).
    • Note: (nprev, valueprev) is optional parameter to provide info that it has previously accepted a proposed value.

Acceptor decision flow chart

paxos acceptor phase 1 decision flow chart.png

Paxos phase 1 Sequence diagram

Paxos-Phase 1.drawio.png

Phase 2 (milestone 2 and 3)

Till now Proposers has received a Promise(n) or Promise(n, (nprev, valueprev)) from a majority of acceptors.

Proposer Now Proposer will attempt to bring consensus on a value by sending an Accept(n, value) message to at least a majority of acceptors, where -n is the proposal number that was promised.

  • If Promise(n), then value is the actual value it wants to propose.
  • If Promise(n, (nprev, valueprev)), then value is the value<sub>prev</sub> that went with the highest nprev.

Acceptor On receiving an Accept(n, value) message; It will decide if it has previously promised to ignore requests with this proposal number.

  • If so, it will ignore the message.
  • Else, it replies with Accepted(n, value), and also sends Accepted(n, value) to all learners.

Paxos-Phase 1.drawio.png

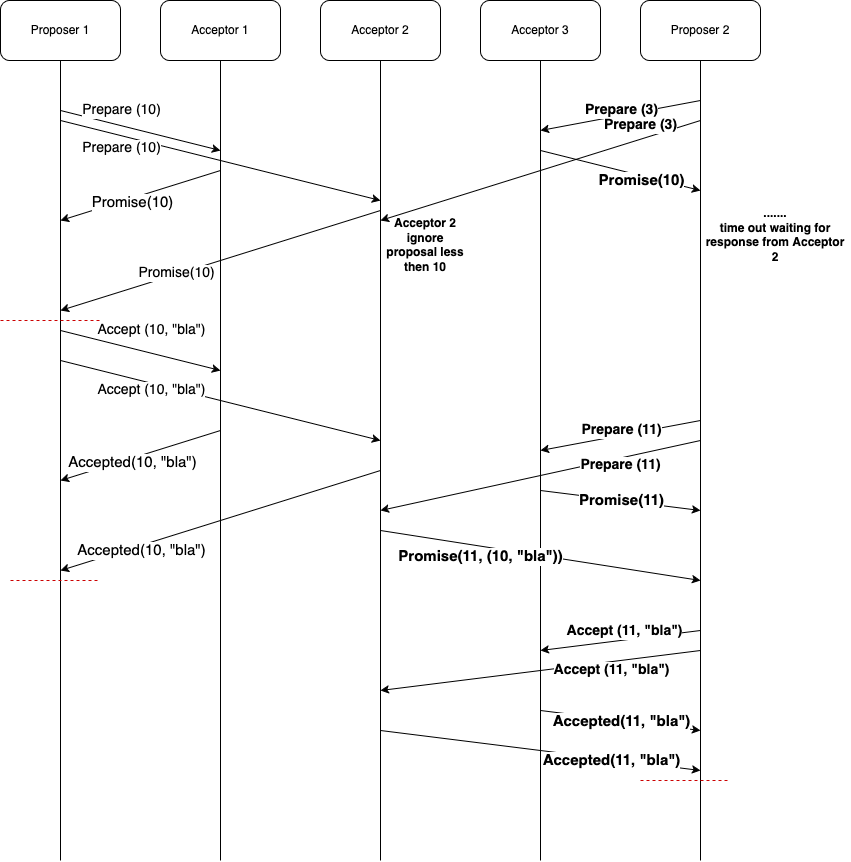
Simple scenario of multiple proposers

In this case there are multiple proposers. Lets assume there are two proposers and they have agreed on some scheme to send unique numbers. For example - proposer 1 says it will send even numbers, and proposer 2 will send odd numbers.

In the bellow case there are two things highlighted:

  1. Proposer times out waiting for acceptors to promise the proposal. It’s a valid case and can happen if acceptor has already promised higher number.
  2. Proposer honours the already accepted value that might have came in from other proposers.

Paxos-Case 1 - multiple proposers.drawio.png

Limitation

  1. Dueling Proposers - As you know from FLP Result that we cannot all three - termination, agreement and validity. In Paxos algorithm we sacrificed termination. This means there can be cases where agreement is never reach, for example when proposer 1 and 2 keep sending higher proposal number before agreement is reached.
  2. Standard Paxos agree on one value. We can ideally modify it to make Multi-Paxos where we can agree on sequence of values for a same agreed upon proposal number (keep on doing phase 2).
  3. We need 2f+1 acceptors to be fault tolerant.

Learnings

References