FLP Impossibility and beyond

We are on a path to build a strong foundation in distributed systems. We have already gone over distributed time; the next topic we will cover is Distributed Consensus. To build the foundation on distributed consensus, we will go over the the paper ‘Impossibility of Distributed Consensus with One Faulty Process’ submitted in 1982 by Fischer, Lynch and Paterson. The purpose to understand this paper is to understand the limitation of distributed systems. The paper essentially presented what’s not possible and whole generation of researchers used it to come up with consensus algorithms by accepting the limitations of the distributed system.

Context

The FLP paper solved a fundamental question that researchers had grappled with regarding consensus in distributed systems. The consensus problem requires all non-faulty processors in a distributed system to agree on a single value. While it was known that consensus could be achieved reliably in synchronous systems (where timing assumptions can be made), the possibility of consensus in asynchronous systems (where no timing assumptions exist) remained an open question.

The FLP paper proved a profound and surprising result: it is impossible to guarantee consensus in an asynchronous distributed system if even a single processor may fail. This impossibility result has become one of the most fundamental theorems in distributed computing.

Basics Of Consensus Protocol

Consensus problem is about getting distributed set of processors to reach agreement in a reasonable time.

A protocol said to solve the consensus problem if it satisfies three key properties simultaneously:

Termination: no matter how the systems runs, every non-faulty processor makes a decision after a finite number of steps;
Agreement: no matter how the system runs, two different non-faulty processors never decide on different values;
Validity: the value that has been decided must be proposed by one of the processors. This is to avoid the trivial solution of always agreeing on a constant.

If the processors and the communication system are completely reliable, the existence of consensus protocols is trivial. The problem becomes interesting when the protocol must operate correctly when some processors can be faulty.

Synchronous consensus

A Synchronous systems means processes run at known rates, and messages are delivered in known bounds of time.

A simple algorithm for synchronous consensus: Each process broadcast its initial value to each processor. In a synchronous network, this can be done in a single “round” of messages. After this round, each process decides on the minimum value it received.

If no fault occurs, above algorithm is correct. The issue occurs if one of the processor fails in between the round. When this happens, some process may have received its initial value, while others may not have.

To make it fault-tolerant to f crashes, we will need f+1 rounds. f+1 because we need at-least 1 round where all the non-faulty processors can broadcast the values to all other processors.

For Example - We want to design for at most 1 processor crash. There will be 2 rounds of consensus. In 1st round, processors broadcast their own initial value. In 2nd round, processors broadcast the minimum value they heard. Each process then decides on the min value among all the sets of values it received in 2nd round.
If the 1 crash happens on 1st round, the 2nd round ensures all processors gets the same set of values. Else if the crash occurs in 2nd round, 1st round would have completed with each processor having same set of values.

Asynchronous System

In completely asynchronous system there is no upper bound on the amount of time processors may take to receive, process, and respond to an incoming message.

The FLP impossibility result proves that in an asynchronous system, no deterministic consensus protocol can guarantee all three properties (Termination, Agreement, and Validity) if even one processor can fail (1-resilient). This is so surprising to me as we cannot reach consensus even if 1 processor just shuts down (fail-stop).

The main reason for FLP result is its impossible to tell if a processor has failed, or is simply taking a long time to do its processing.

NOTE: The FLP result does not state that consensus can never be reached. It merely tells that under the asynchronous model’s assumptions, no deterministic algorithm can always reach consensus in bounded time.

Simplified explanation of proof presented in FLP paper

The proof’s foundation rests on the concept of bivalent states - system configurations where both 0 and 1 remain possible as final decisions. A state is 0-valent when all possible futures lead to deciding 0, and 1-valent when all futures lead to deciding 1.

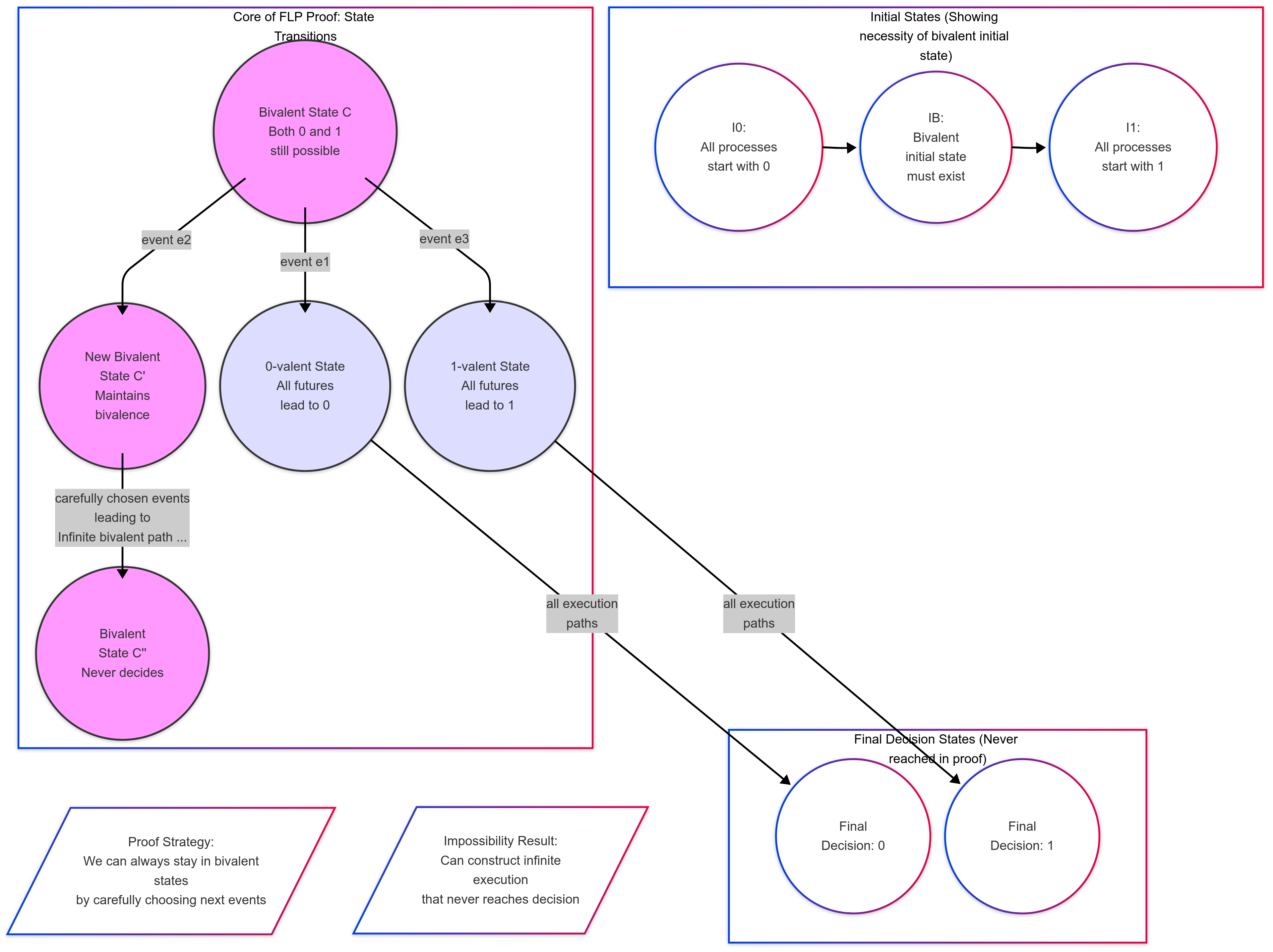
FLP Impossibility.png

To start our proof, we show a bivalent initial state must exist. Imagine a scenario where some processes start with 1 and others with 0. If all processes with input 1 crash immediately, validity requires deciding 0. Similarly, if all processes with 0 crash, the system must decide 1. Between these two extremes, there must be an initial configuration that’s bivalent - if not, we’d have adjacent initial states leading inevitably to different decisions, violating agreement.

Now comes the proof’s core: from any bivalent state, we can always maintain bivalence through careful scheduling. Consider a bivalent configuration C and any possible next step e by some process p. If executing e would make the system univalent, we can always find another step e’ that either keeps the state bivalent or leads to the opposite decision. This works because asynchrony lets us reorder events and delay messages arbitrarily.

The key insight exploits this asynchrony combined with potential failures. When a process is about to take a decisive step, we can postpone it and let another process move first. Since we can’t distinguish between a crashed process and one that’s just slow, no process can safely wait for another. This lets us construct an infinite execution that never leaves bivalent states by carefully choosing which events happen next.

This infinite bivalence directly contradicts consensus’s termination requirement. We’ve proven any consensus protocol must have at least one execution where some correct process never decides. The result’s power lies in its universality - it applies to any possible consensus protocol, showing a fundamental limitation rather than a mere algorithmic weakness.

The impossibility emerges from a fundamental tension: processes must wait long enough to agree but decide quickly enough to terminate. In an asynchronous system with failures, this tension cannot be resolved. No protocol can simultaneously guarantee safety (agreement and validity) and liveness (termination). This core result shapes modern distributed systems design, forcing engineers to either relax asynchrony assumptions or accept that guaranteed consensus is impossible.

Beyond FLP Result

The work from Dolev, et al in paper “On the Minimal Synchronism Needed For Distributed Consensus” builds up on the FLP result. He goes a step forward into breaking down the asynchrony characteristics to find the minimal cases where N-resilient consensus protocol exists.

He breaks down the problem into 5 characteristics :

Processors synchronous or asynchronous
Communication synchronous or asynchronous
Message order synchronous or asynchronous
Broadcast transmission or point to point transmission
Atomic receive/send or separate receive and send

Varying these 5 parameters there are 32 cases and out of those there are 4 cases where N-resilient consensus protocol exists -

synchronous processors and synchronous communication - This is the classic Sync protocol already discussed above.
synchronous processors and synchronous message order - Even with unbounded message delays, when processors operate in lock-step and messages are delivered in a consistent order, processes can wait for messages in a deterministic way. The synchronous processors ensure no one gets too far ahead, while ordered messages prevent confusion about message sequence, enabling agreement despite asynchronous communication.
broadcast transmission and synchronous message order - This case shows the power of broadcast with ordered delivery. Even with asynchronous processors and communication, when all processes receive the same messages in the same order (like a perfect shared log), consensus becomes possible. It’s similar to having a perfect sequencer that everyone trusts to order events.
synchronous communication, broadcast transmission, and atomic receive/send - This combination leverages atomic operations with bounded communication delays and broadcast. The atomic receive/send prevents any gaps in message handling, broadcast ensures everyone gets the same messages, and synchronous communication provides timing guarantees. Together, these properties enable consensus even with asynchronous processors and message ordering.

The basic intuition used by author to come up with above cases is: If letting t processes fail can effectively “hide” an event or the relative ordering among several events, then no consensus protocol is t-resilient.

“Fixing” FLP - Scenarios where consensus can be solved

Consensus solvable space in distributed systems can be categorized into four main approaches, each making different trade-offs to achieve agreement among processes.

Synchronous System - Synchronous Systems represent the classic and most straightforward approach to consensus. In these systems, processors operate in lock-step with bounded message delivery times, enabling round-based protocols with fixed durations. While this approach offers clear deterministic guarantees and simple failure detection mechanisms, it’s often impractical in real-world networks due to its strict timing requirements and vulnerability to timing violations.
Partially Synchronous Systems with Failure Detectors - As demonstrated in Chandra’s seminal 1996 paper, failure detectors effectively bridge the gap between synchronous and asynchronous systems by abstracting timing assumptions into failure detection mechanisms. This approach breaks the FLP impossibility result by providing additional information that helps distinguish between slow and crashed processes. The concept of ◇W (Eventually Weak) failure detector proved to be the weakest detector capable of solving consensus, establishing a fundamental theoretical foundation.
Approximate Agreement - introduced in Dolev’s 1986 paper, takes a different approach by relaxing the agreement condition. Instead of requiring processes to agree on exactly the same value, this method allows correct processes to decide on values within a bounded range. This relaxation makes the protocol particularly suitable for practical applications like sensor networks, load balancing, and distributed control systems, where exact agreement isn’t necessary and some variance is acceptable.
Probabilistic Termination - pioneered by Ben-Or’s 1983 paper, addresses consensus by relaxing the termination condition. While deterministic solutions are impossible in asynchronous systems (due to FLP), probabilistic algorithms can achieve consensus with high probability. Ben-Or’s original algorithm, though requiring O(2^n) expected rounds, demonstrated that randomization could circumvent the impossibility result. Modern implementations have significantly improved efficiency through shared coin protocols and other optimizations.

Learnings

The most powerful learning for me was how useful impossibility proofs are. This FLP impossibility paper is the foundation over which all the future consensus protocols are built upon. Once we know what’s impossible, we can start working toward plausible cases by tweaking the parameters to break the impossibility proof. Most importantly this helps us in arguing about the system we are building, and defining what the system actually guarantees.

Other learnings are

Trade-offs - In system design and in life all decisions are about trade-offs. Many protocols such as Ben-Or’s 1983 paper are results of trade-offs and defining the system model that slightly tweaks the model to break FLP impossibility.
While reading or building consensus protocols we can decompose it to termination, agreement and validity.
Few system design thinking models -
- Failure detection is always probabilistic
- Bounded queues, bounded time, bounded everything :) is most powerful technique in overcoming long outages and breaking impossibilities.
- Defining System specs before jumping into can we do xyz -> yeah problem solve, dry run passed :) -> design complete -> design review -> hammered by PEs (good/real ones) :( . PS: yeah its not design complete -> product launch, hahaha.
- Defining the system behavior when impossible situation appears is very important for recovery. Or you can end up with servers doing no real work, or end up in playing long game of “servers will catch up in next 2 hrs, maybe”.
- Monitoring is important to know when our assumptions in system spec is breaking.